Solving the Gierer-Meinhardt model using Julia
Learning how to discretize and solve a reaction-diffusion system in Julia
Solving the Gierer-Meinhardt model using Julia
The Gierer-Meinhardt model is defined as follows:
$$ \frac{\partial u}{\partial t} = D_u \Delta u + \rho\frac{u^2}{v} - \mu_u u + \rho_u $$
$$ \frac{\partial v}{\partial t} = D_v \Delta v + \rho u^2 - \mu_v v + \rho_v, $$
with
- $u$ being a short-range autocatalytic substance, or in other words, an activator,
- $v$ being its long-range antagonist, or in other words, an inhibitor, and,
- $\Delta = \sum\limits_{i = 1}^{n} \frac{\partial^2}{\partial x_i^2}$ being the n-dimensional Laplace operator.
In the Gierer-Meinhardt equations, the autocatalytic substance activates both itself and the inhibitor substance (with rate $\rho u^2)$, whereas the inhibitor function inhibits the growth of the autocatalytic substance (with rate $\frac{1}{v})$. Both substances have a natural decay rate of the form $\mu_u u$ and $\mu_v v$ respectively. Finally, both substances have an activator-independent production rate ($\rho_u$ and $\rho_v$).
For the right choice of parameters, pattern formation can be observed in the solution of the Gierer-Meinhardt model.
More info on the Gierer-Meinhardt model can be found in this scholarpedia article.
Solving the system
We’ll solve the following IBVP:
$$ \frac{\partial u}{\partial t} = D_u \Delta u + \rho\frac{u^2}{v} - \mu_u u + \rho_u $$
$$ \frac{\partial v}{\partial t} = D_v \Delta v + \rho u^2 - \mu_v v + \rho_v $$
$$ u(x,y,0) = \exp{\left(-(x-a)^2-(y-a)^2\right)}, \quad \forall (x,y) \in (0,L)^2$$ $$ v(x,y,0) = {\rm rand}(), \quad \forall (x,y) \in (0,L)^2$$ $$ \frac{\partial u}{\partial n}(x,0,t) = \frac{\partial v}{\partial n}(x,0,t) = 0, \quad \forall x \in [0,L]$$ $$ \frac{\partial u}{\partial n}(x,L,t) = \frac{\partial v}{\partial n}(x,L,t) = 0, \quad \forall x \in [0,L]$$ $$ \frac{\partial u}{\partial n}(0,y,t) = \frac{\partial v}{\partial n}(0,y,t) = 0, \quad \forall y \in [0,L]$$ $$ \frac{\partial u}{\partial n}(L,y,t) = \frac{\partial v}{\partial n}(L,y,t) = 0, \quad \forall y \in [0,L] .$$
We start by initializing the parameters
Du = 1;
Dv = 100;
ρ_u = 0.5;
ρ_v = 0;
ρ = 1;
μ_u = 1;
μ_v = 6.1;
a = 5;
L = 100;
Then, we discretize the 2D space grid
sizez = L; # size of the 2D grid
dx = 100.0 / sizez; # space step
and then we discretize time
T = 150.0; # total time
dt = 0.0003; # time step
n = floor(Int, (T / dt)); # number of iterations
nvis = 500; # saves every nvis time steps
Next we use a random seed in order for the results to be the same across multiple runs and set the initial conditions
using Random
Random.seed!(1)
U = [exp(-(x-a)^2-(y-a)^2) for x in 1:1:sizez, y in 1:1:sizez];
V = rand(sizez, sizez);
Consequently, we initialize two matrices for the inside of the grid, and five matrices that will help us compute the Laplacian
Uc = zeros(Float64, sizez - 2, sizez - 2);
Vc = copy(Uc);
Ztop = copy(Uc);
Zleft = copy(Uc);
Zbottom = copy(Uc);
Zright = copy(Uc);
Zcenter = copy(Uc);
Finally, we initialize a 3D matrix, in order to save $u$ every $nvis$ time steps
UR = zeros(sizez, sizez, floor(Int, n/nvis));
We define a function in order to discretize the Laplacian, using the broadcasting abilities of Julia and the @views macro.
@views function DLaplacian(Z) # Centered differences discretization of the Laplacian
Ztop .= Z[1:end-2, 2:end-1]
Zleft .= Z[2:end-1, 1:end-2]
Zbottom .= Z[3:end, 2:end-1]
Zright .= Z[2:end-1, 3:end]
Zcenter .= Z[2:end-1, 2:end-1]
return (Ztop .+ Zleft .+ Zbottom .+ Zright .- 4 .* Zcenter) ./ (dx^2)
end
DLaplacian (generic function with 1 method)
We then proceed to iterate the solution beginning from the second timestep and ending in timestep $n$.
@views begin
j = 1
for i in 2:n
Uc .= U[2:end-1, 2:end-1]
Vc .= V[2:end-1, 2:end-1]
U[2:end-1, 2:end-1] .= Uc .+ dt .* (Du .* DLaplacian(U) .+ ρ_u .- μ_u .* Uc .+ ρ.* (Uc.^2)./Vc )
V[2:end-1, 2:end-1] .= Vc .+ dt .* (Dv .* DLaplacian(V) .+ ρ_v .- μ_v .* Vc .+ ρ.* Uc.^2 )
for Z in (U, V) # Neumann boundary conditions
Z[1, :] .= Z[2, :]
Z[end, :] .= Z[end-1, :]
Z[:, 1] .= Z[:, 2]
Z[:, end] .= Z[:, end-1]
end
if i%nvis == 0
UR[:,:,j] .= U
j += 1
end
end
end
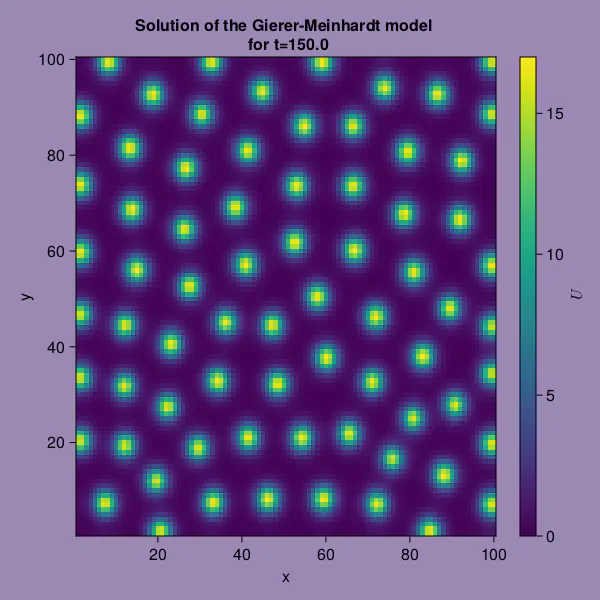
We notice interesting spot-like patterns in the solution for $t = 1000 \cdot dt \cdot nvis$
using CairoMakie
joint_limits = (0, 17)
time_step = 1000
time = time_step * dt * nvis
fig = Figure(backgroundcolor = "#9B89B3",
resolution = (600, 600))
ax = Axis(fig[1,1],
title = "Solution of the Gierer-Meinhardt model \n for t=$(time)",
xlabel = "x",
ylabel = "y")
hmr = CairoMakie.heatmap!(ax, UR[:,:,time_step])
Colorbar(fig[:,end+1], colorrange = joint_limits, label = L"U")
fig
Of course, if we want to speed things up, we’ll want to wrap the above code in a function
using Random
@views function GiererMeinhardt()
Du = 1;
Dv = 100;
ρ_u = 0.5;
ρ_v = 0;
ρ = 1;
μ_u = 1;
μ_v = 6.1;
a = 5;
L = 100;
nvis = 1000
sizez = 100 # size of the 2D grid
dx = 100.0 / sizez # space step
T = 150.0 # total time
dt = 0.0003 # time step
n = floor(Int, (T / dt)) # number of iterations
Uc = zeros(Float64, sizez - 2, sizez - 2)
Vc = copy(Uc)
Ztop = copy(Uc)
Zleft = copy(Uc)
Zbottom = copy(Uc)
Zright = copy(Uc)
Zcenter = copy(Uc)
Random.seed!(1)
U = [exp(-(x-a)^2-(y-a)^2) for x in 1:1:sizez, y in 1:1:sizez]
V = fill(1.0, sizez, sizez)
UR = zeros(sizez, sizez, floor(Int, n/nvis))
function DLaplacian(Z) # Centered differences discretization of the Laplacian
Ztop .= Z[1:end-2, 2:end-1]
Zleft .= Z[2:end-1, 1:end-2]
Zbottom .= Z[3:end, 2:end-1]
Zright .= Z[2:end-1, 3:end]
Zcenter .= Z[2:end-1, 2:end-1]
return (Ztop .+ Zleft .+ Zbottom .+ Zright .- 4 .* Zcenter) ./ (dx^2)
end
j = 1
for i in 2:n
Uc .= U[2:end-1, 2:end-1]
Vc .= V[2:end-1, 2:end-1]
U[2:end-1, 2:end-1] .= Uc .+ dt .* (Du .* DLaplacian(U) .+ ρ_u .- μ_u .* Uc .+ ρ.* (Uc.^2)./Vc )
V[2:end-1, 2:end-1] .= Vc .+ dt .* (Dv .* DLaplacian(V) .+ ρ_v .- μ_v .* Vc .+ ρ.* Uc.^2 )
for Z in (U, V)
Z[1, :] .= Z[2, :]
Z[end, :] .= Z[end-1, :]
Z[:, 1] .= Z[:, 2]
Z[:, end] .= Z[:, end-1]
end
if i%nvis == 0
UR[:,:,j] .= U
j += 1
end
end
return UR
end
resG = GiererMeinhardt();
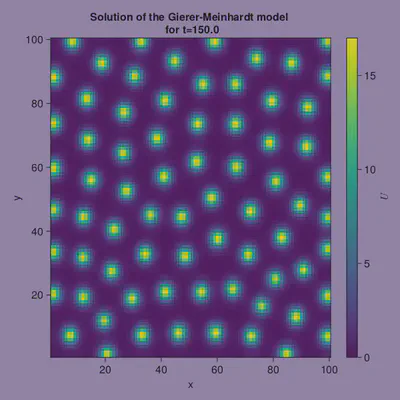
Finally, we make a nice little video illustrating how the pattern formed
using CairoMakie
joint_limits = (0, 17)
fig = Figure(backgroundcolor = "#9B89B3",
resolution = (600, 600))
ax = Axis(fig[1,1],
title = "Solution of the Gierer-Meinhardt model",
xlabel = "x",
ylabel = "y")
hmr = CairoMakie.heatmap!(ax, resG[:,:,1])
Colorbar(fig[:,end+1], colorrange = joint_limits, label = L"U")
fig
nframes = 10
framerate = 30
iterator = 1:2:500
output_gif = record(fig, "GiererMeinhardt.mp4", iterator;
framerate = framerate) do t
CairoMakie.heatmap!(ax, resG[:,:,t], colorrange = joint_limits)
end
Of course, different initial conditions and parameter values, will change the behavior of the model. So, copy the code and do some experimenting!
Vasilis Tsilidis
PhD Student
My research interests include Mathematical Biology, Dynamical Systems and Machine Learning.